Wolfram mathematica для интерактивной визуализации задач начертательной геометрии
Решаемая проблема. Контекстуализация WM в процесс геометро-графической подготовки студентов вуза, через создание собственных WM – проектов, представляющих собой наглядную, в виде интерактивных графиков, визуализацию решения задач курса НГ.
Методы исследования. Методы интеллектуальных и информационных средств решения задач символьной системы WM; интерпретируемый язык функционального программирования Wolfram (Wolfram Language) пакета символьной математики WM.
Детали исследования. В ходе исследования проведён анализ существующих и ранее реализованных WM-проектов, близких к тематике исследования. Компания Wolfram Research с целью демонстрации возможностей системы и приёмов программирования на языке Wolfram, а также расширения круга пользователей создала систематизированный каталог свободно распространяемых онлайн WM –проектов и интерактивных демонстраций программных приложений. Каталог регулярно обновляется, в нём размещены и находятся в свободном доступе демонстрации из разных разделов (модулей), иллюстрирующих решения задач, поясняющие процессы и понятия из широкого диапазона областей.
Выраженные через элементы графики выходные данные WM–проекта на построение линии пересечения двух плоскостей WM-проект («1_2_Planes»), визуально представляют пользователю построение плоскостей, и, соответственно, линий их пересечения через уравнения поверхностей ax + bx + cx = d. Каждая плоскость задаётся через 4 параметра: коэффициенты: а, b, c и d. Построения ведутся с помощью уравнений поверхностей, предоставляя пользователю возможность изменять коэффициенты уравнения а, b, c и d с помощью ручек-манипуляторов, тем самым перестраивать пересекающиеся плоскости, и, соответственно, линию их пересечения. Для усиления эффекта наглядности линия пересечения плоскостей выделена с помощью яркой салатовой линии (рис. 1).

Рис. 1 – WM–проект «1_2_Planes». Установлена максимальная интенсивность плоскостей проекций, показаны пересекающиеся плоскости, линия их пересечения и следы плоскостей
Основная сложность при работе через уравнения поверхностей была в необходимости добиться того, чтобы при динамическом изменении изображаемых плоскостей, линии пересечения плоскостей также динамично менялись. При работе с уравнениями поверхностей, линии пересечения плоскостей задаются через регионы, но, в том случае, когда линий много, изображение пересчитывается дольше и график «подвисает».
Что касается взаимодействия плоскости с поверхностью, то плоскость определяется через функцию «Infinite line», внутри которой заданы параметры плоскости. Данный способ почти полностью аналогичен заданию плоскости через функцию «CounterPlot3D». В графиках такого типа выделяется только линия пересечения поверхности с плоскостью (красным цветом) (рис. 2, 3). Это делается с помощью функции «MeshFunction» внутри функции «CounterPlot3D». Хотелось бы выделить отдельным цветом эту линию и другим цветом линии пересечения поверхности с плоскостями проекций. В данный момент это пока не удаётся.
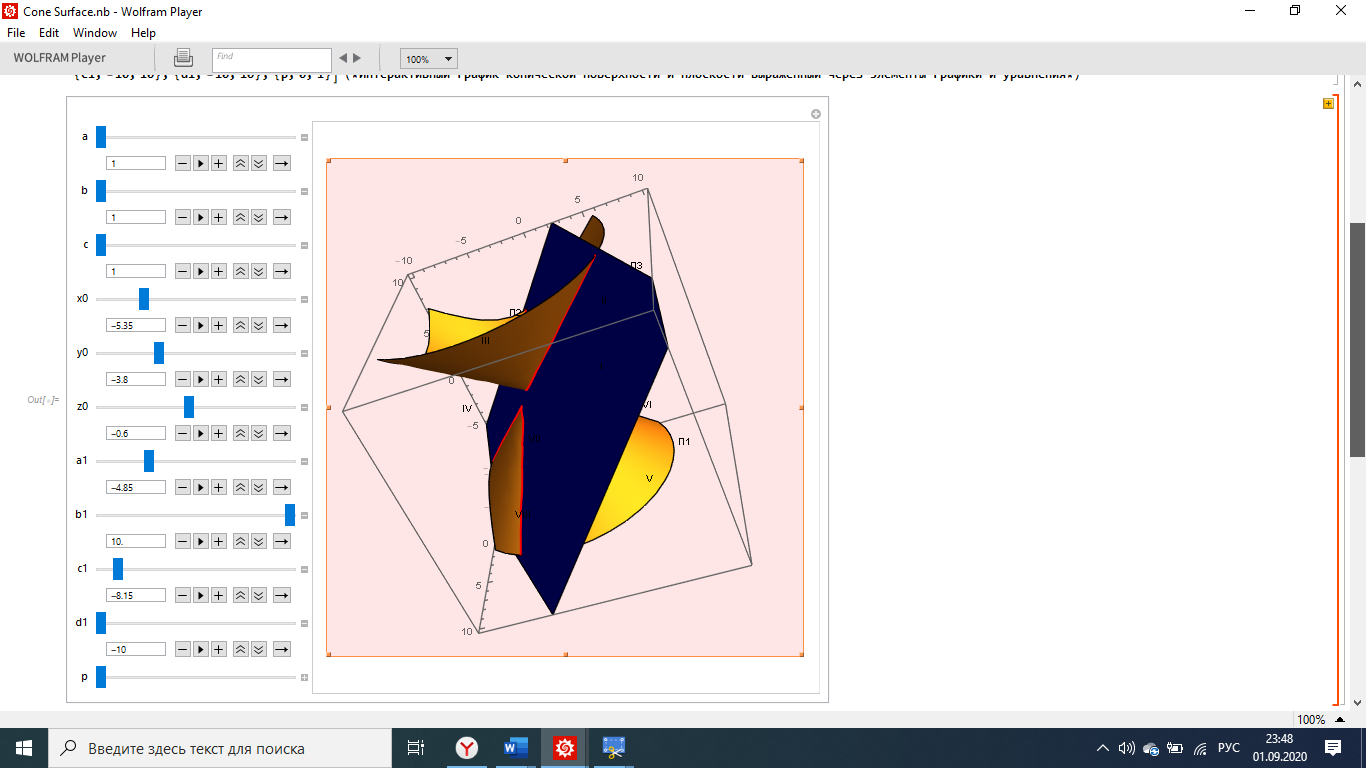
Рис. 2 – WM–проект «Взаимное положение плоскости и конической поверхности» (WM-проект 3_1_Cone Surface)
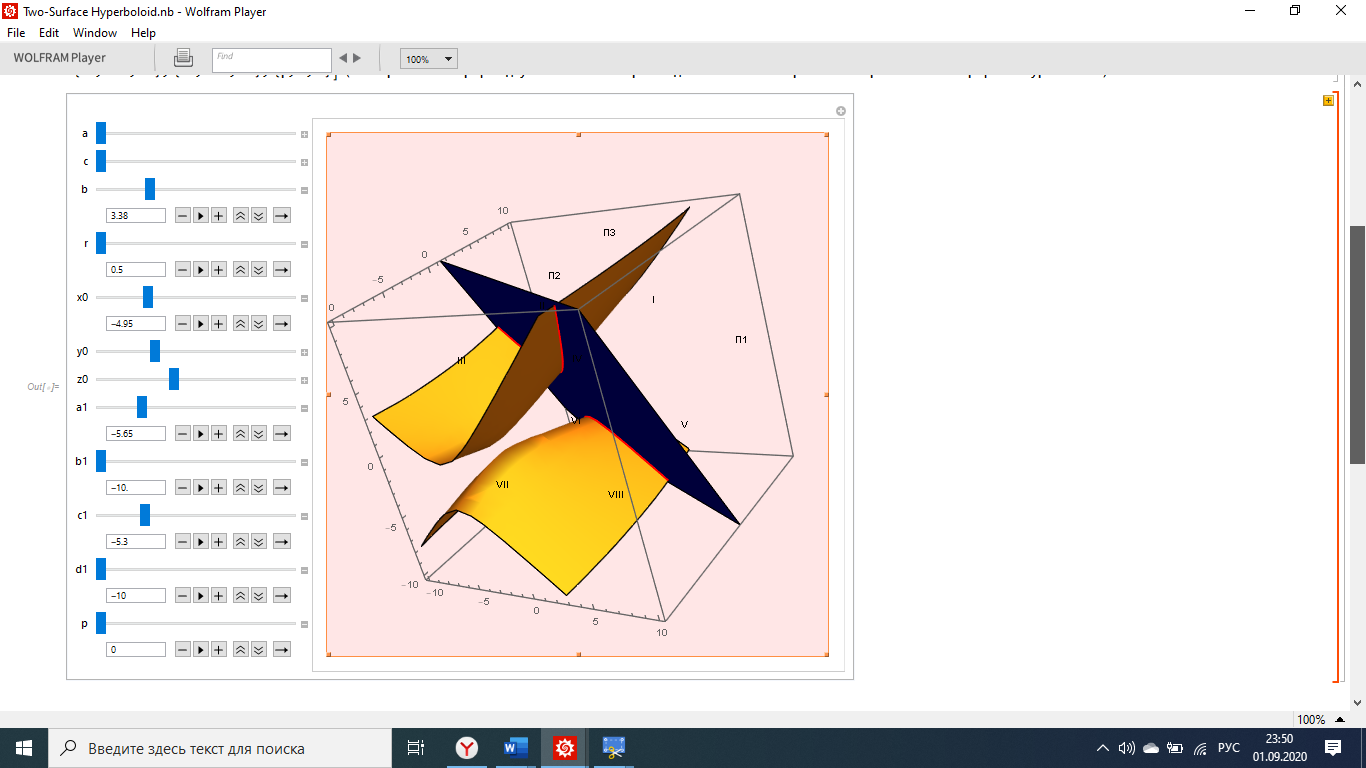
Рис. 3 – WM–проект «Взаимное положение плоскости и поверхности двуполостного гиперболоида» (WM-проект 3_8_Two-Surface Hyperboloid)
Заключение. В результате проведённой работы реализована задача и достигнута цель исследования, а именно, выявлена возможность контекстуализации программного продукта WM в процесс геометро-графического обучения студентов. Созданы, реализованы и предлагаются к обсуждению исходные коды и выходные данные собственных интерактивных, статических и динамических WM – проектов, представляющих собой наглядную, в виде интерактивных графиков, визуализацию решения базовых задач курса начертательной геометрии (НГ), сгруппированных в 7 разделов.
Выявлены преимущества WM над другими специализированными математическими программными пакетами, а также сложности, возникшие в работе, идеи и возможности дальнейшего внедрения предлагаемых принципов использования вычислительных алгоритмов WM при создании и использовании WOLFRAM – проектов в процессе геометро-графической подготовки студентов.

