Математическое моделирование функционирования детандер-генераторного регулятора давления в нестационарных условиях малых пунктов редуцирования
Существующая проблема. Дальние расстояния транспортировки газа обуславливают высокое давление перекачки, которое требуется снижать перед отправкой потребителю. Снижение происходит на пунктах редуцирования путём расходования энергии потока природного газа на преодоление местного сопротивления, представленного дроссельным органом регулятора давления. Эта энергия может быть направлена на полезное использование, но реализация такого утверждения для малых пунктов редуцирования давления осложнена, так как при приближении к конечным потребителям существенно растут величины нестационарностей, падают расходы и давления газа. Также снижаются требуемые для систем самих пунктов редуцирования электрические мощности, а поиск сторонних потребителей электроэнергии становится сложнее. Всё это серьёзно ограничивает применение различных энергоутилизационных технологий с точки зрения их технико-экономических показателей.
Идея работы. В данной работе предлагается замена дроссельных регуляторов давления малых пунктов редуцирования детандер-генераторными регуляторами, основанными на расширительных машинах объёмного типа. Представлены две схемы реализации таких устройств.
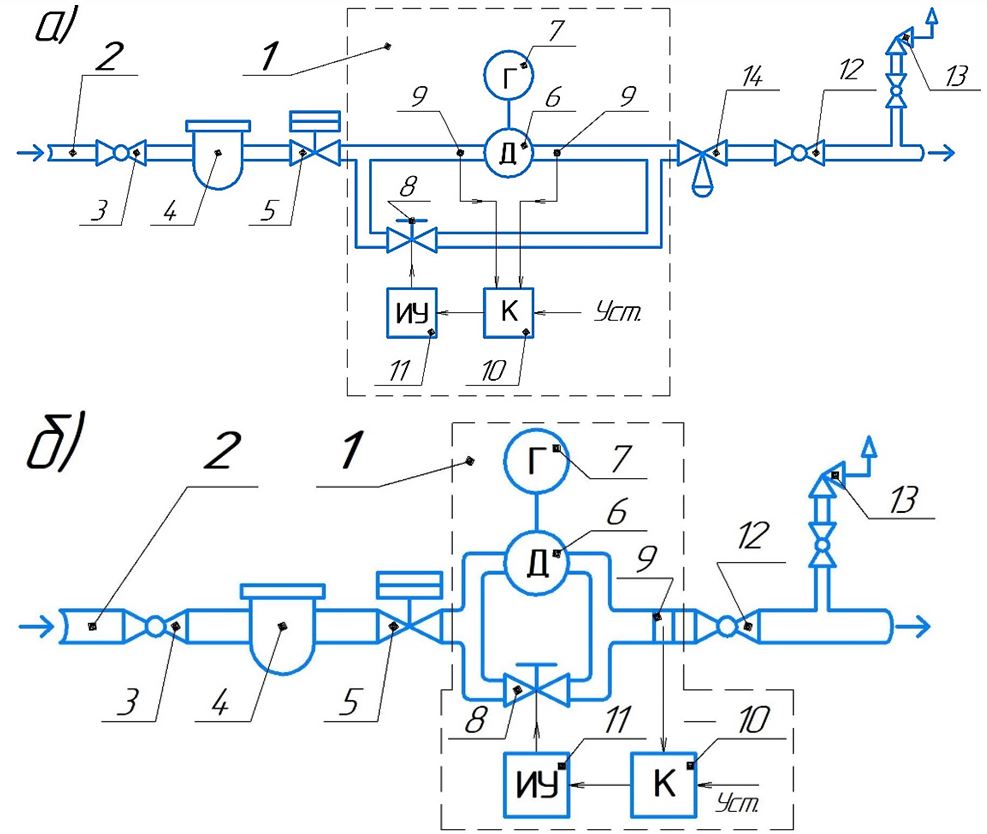
Рис. 1. Принципиальная схема линии редуцирования газа на пункте редуцирования с системой ДГР расширительного типа со стабилизацией системой регулирования: а) перепада давления до и после детандера; б) давления на выходе из ПРГ.1 – ДГР;2 – линия редуцирования; 3 – входная запорная арматура;4 – фильтр; 5 – ПЗК; 6 – объемный детандер;7 – электрогенератор; 8 – регулирующий клапан; 9 – датчик давления;10 – контроллер; 11 – исполнительное устройство регулирующего клапана;12 – выходная запорная арматура; 13 – ПСК; 14 – РД
Детали исследования. Полученная математическая модель является объединением констант и исходных данных, вспомогательных уравнений, дифференциальных уравнений и их начальных условий, и логических условий [26]. Также применяются логические условия, моделирующие вращение ротора объемной машины и сохраняющие изменяющиеся параметры в заданном диапазоне. Используются различные конструкции реализации ПИД-сигнала управления в вариантах работы системы стабилизации а и б.
Таким образом, система основных дифференциальных уравнений имеет вид:

Чтобы проверить устойчивость системы ДГР в условиях нестационарностей было задано несколько ступенчатых возмущений.
Заключение. Разработана математическая модель процесса детандерного редуцирования, позволяющая рассчитать газодинамические параметры газа и механические – детандера, работающего в нестационарных условиях. Она может быть использована, как часть методики по подбору параметров объёмных детандеров, предназначенных для работы в малых пунктах редуцирования.
Возможность стабильной работы расширительного ДГР и предложенных систем стабилизации в условиях неравномерностей отбора газа потребителями и изменений давления на входе в ПРГ подтверждена математическим моделированием. Приоритетной является схема б, когда детандер-генератор выступает одновременно в качестве утилизационной установки и регулятора давления.

